RESOLUT

• The program resolut.exeand a library (to write to the same directory).

• The input file d3l_3_2.txt for the dihedral algebra of the family D(3L) with the parameters k=3, s=2.

• The input file d3q_2_3_4.txtfor the dihedral algebra of the family D(3Q) with the parameters k=2, s=3, t=4.

• The input file d3r_2_8_6_4.txt for the dihedral algebra of the family D(3R) with the parameters k=2, s=8, t=6, u=4.

The program is implemented in Borland C++ Builder for Microsoft Windows. It reads a file defining a quiver with relations and constructs the corresponding algebra. It computes the bases and finds the diagrams of indecomposable projective modules over the algebra. The main objective of the program is to compute the minimal projective resolutions of simple modules. For now, the program works for most dihedral and some semi-dihedral algebras. For every simple module Si the algorithm tries to construct a bicomplex such that its total complex gives the minimal projective resolution of Si.

The program window has 8 buttons and a text output area. They are used as follows:

• Define quiver button allows to read a data file describing a quiver with relations and to start the computation. Previously loaded and computed data is overwritten.

• Diagrams button shows the diagrams of the indecomposable projective modules over the algebra.

• Print diagrams button allows to print the window with the diagrams of the indecomposable projective modules.

• Bicomplex S0 ... Bicomplex S2 buttons show the constructed bicomplexes for the simple modules S0 ... S2 of the indecomposable projective modules over the algebra. The first 10 diagonals of the bicomplexes are computed automatically. A double click in the bicomplex window allows to compute one more diagonal.

• Print bicomplex button prints the currently shown bicomplex window.

• Result file button writes the computation results to the file Res.txt. Other intermediate files are also created during the computation.

• The text area shows the bases and dimensions of the indecomposable projective modules over the algebra.

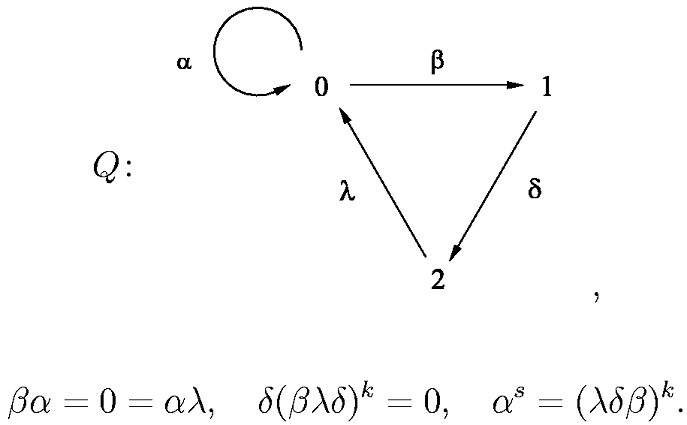
To read a data file, press the button Define quiver. Let us describe the input file format using the example of an algebra of the family D(3L). These algebras are defined by the following quiver with relations (k>1, s>1):

We write the composition from the right to the left. Let us give an example of an input file, the file d3l_3_2.txt .  It describes the dihedral algebra of the family D(3L) with the parameters k=3, s=2. We replace \alpha by a, \beta by b etc.

The input quiver with relations must be described as follows:

• The number of vertices in the quiver in the following format:
  AllKnotsNum=<number>

• The number of edges in the quiver in the following format:
  AllEdgesNum=<number>

• The list of AllEdgesNum edges (one edge per line) in the following format:
  <name_letter>,<edge_beginning>,<edge_end>

• The maximal word length in the following format:
  MaxWordLen=<number>
  This is a technical parameter which is not be described here in detail. It can be smaller for smaller values of parameters and must be greater for greater ones.

• The number of relations of the form <monomial>=0 in the following format:
  NulStrsNum=3

• The list of NulStrsNum relations of the form <monomial>=0(one monomial per line) in the following format:
  <monomial>

• The number of relations of the form <monomial_1>=<monomial_2> in the following format:
  RelatsNum=<number>

• The list of RelatsNum relations of the form <monomial_1>=<monomial_2> (one relation per line) in the following format:
  <monomial_1>=<monomial_2>

• The following lines are ignored.

When the file d3l_3_2.txt is loaded, the program window can look like the following:

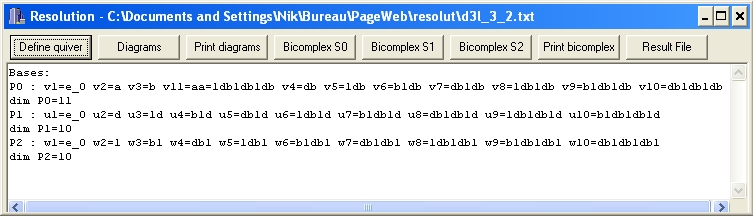
The text in the window gives the bases of the indecomposable projective modules Pi and their dimensions. Inside the program, the basis elements of P1, P2, P3 are denoted as v, u, w with indexes. Their monomial representation is also given.

Press the Diagrams button to see the diagrams of Pi's:

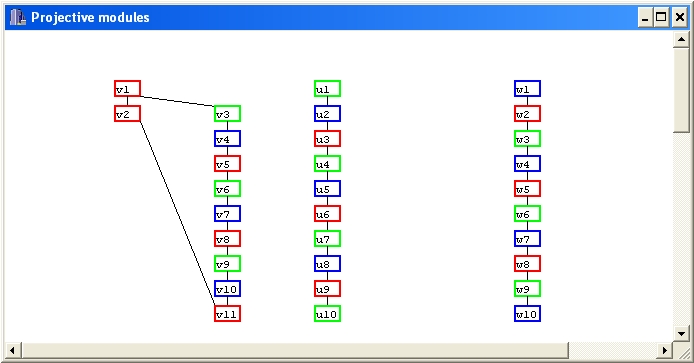
In mathematical notation, these diagrams (for any parameters) can be written as follows:

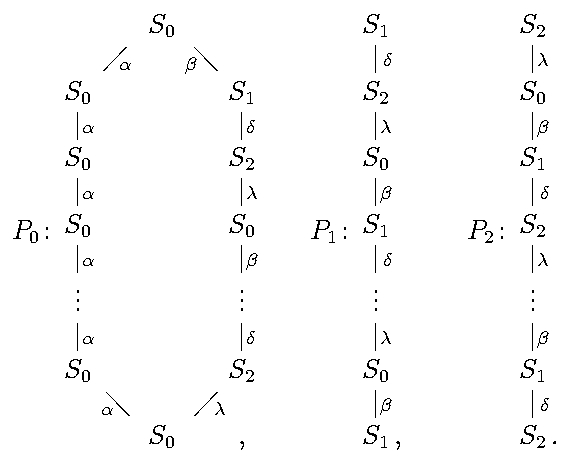
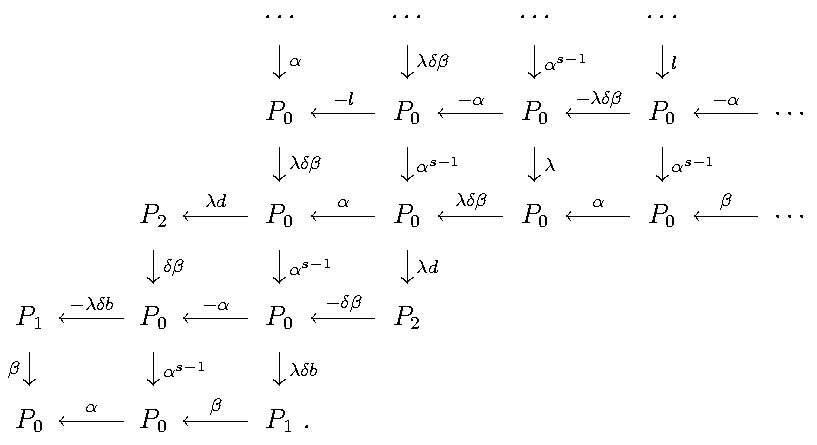
Press the Bicomplex S0 button to see the bicomplex for S0 (its total complex gives the minimal projective resolution of the simple module S0 ):

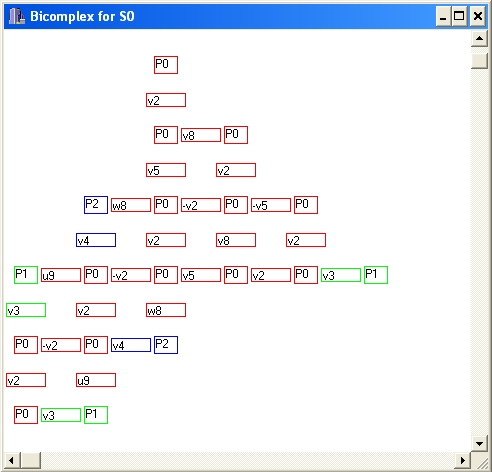
In mathematical notation, this bicomplex can be written as follows (we write it in general, for any parameters, transpose and put the minus signs everywhere in the odd strings to get an anti-commutative bicomplex):